본 글에서는 주어진 데이터에 선형회귀 곡선을 그리고, 그것의 파라미터들 및 선형회귀로 가정한 값들과 실제 값들의 차이를 살펴본다
다음 선형회귀 곡선을 정규화해 위의 작업을 다시 한 번더 실행 그리고 잔차를 살펴본 후, Cross-Validation을 통해 위의 과정을 다시한 번 더 했을떄 잔차값들이 어떻게 변하는지 살펴보는 시간을 갖는다
우선 Python에 있는 sklean의 모듈에 datasets를 불러와 load_boston이라는 데이터를 불러온다
sklearn.linear_model에서 LinearRegression의 모듈을 불러와, 이것을 이용해 선형회귀 곡선의 예측값 및 파라미터들을 살펴본다
from sklearn import datasets
boston = datasets.load_boston()
from sklearn.linear_model import LinearRegression
lr = LinearRegression()
lr.fit(boston.data, boston.target)
predictions = lr.predict(boston.data)
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
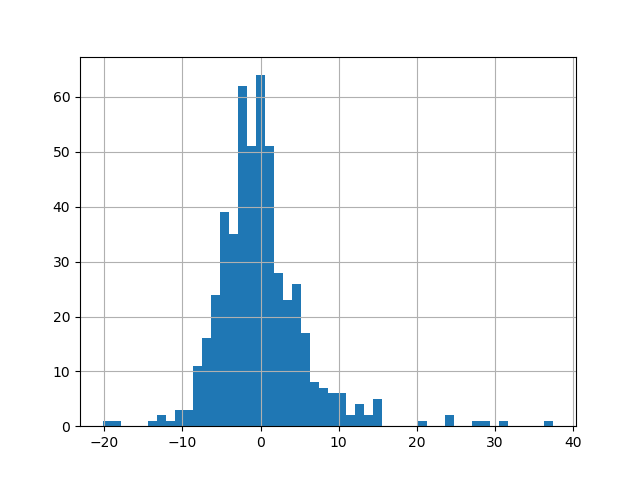
pd.Series(boston.target - predictions).hist(bins=50)
plt.show()
lr.coef_ # 각 종속변수의 파라미터
lr.intercept_ # 회귀분석의 상수값
dir(lr) #여기서 dir은 lr에 어떠한 메소드가 있는지 확인하기 위한 함수
dir(lr)

이번에는 위와 같이 선형회귀 분석을 하되, 정규화를 한 후 똑같이 실행을 할 것이다. 이것을 하는 이유는 정규화를 하면 Error Value(실제값 - 예측값(모델값))이 과역 더욱 정규화가 되는지 살펴보기 위함이다.
lr2 = LinearRegression(normalize=True)
lr2.fit(boston.data, boston.target)
predictions2 = lr2.predict(boston.data)
pd.Series(boston.target - predictions2).hist(bins=50)
plt.show()

정규화를 통한 것과 그렇지 않은 것을 비교했을 때, 그렇게 큰 차이가 보이지는 않는다. 이번에는 Cross-Validation을 통한 선형회귀분석을 실행해본다.
여기서 Cross-Validation을 간략히 설명하면, 통계학에서 모델을 평가하는 방법(Overfitting을 방지하기 위한 도구)으로 Train Data Set을 균등하게 K개의 그룹으로 나누고, K-1개의 Test Fold와 Validation Fold로 지정, 총 K회 검증을 하며 각 검증마다 Test Fold를 다르게 지정하여 성능을 측정하고 이런식으로 K회 검증이 완료되면 Hyperparameter에 평균하여 나타낸 것을 의미한다.
from sklearn import datasets
boston = datasets.load_boston()
from sklearn.linear_model import LinearRegression
lr = LinearRegression()
lr.fit(boston.data, boston.target)
from sklearn.model_selection import cross_val_predict
predictions_cv = cross_val_predict(lr, boston.data, boston.target, cv=10)
pd.Series(boston.target - predictions_cv).hist(bins=50)
plt.show()
'Python > Sklearn for ML' 카테고리의 다른 글
| 5 - LASSO Regression & Parameters(라소 회귀분석에 대하여 및 파라미터 선택) using Python (0) | 2020.03.29 |
|---|---|
| 4 - Penalty(About Overfitting) (0) | 2020.03.07 |
| 3 - About Ridge Regression(리지 회귀분석에 대하여) & Optimizing the Parameter(계수 최적화) with Python (0) | 2020.03.01 |
| 2 - 선형회귀 분석의 단점과 보완방법 (about Over Fitting & Ridge Regression) (0) | 2020.01.04 |



