본 포스팅에서는 지난번 포스팅(1 - Linear Regression with Python)에서 다루었던 내용을 다시 살펴보고, 선형회귀분석의 단점과 단점을 보완하기 위한 방법 중의 하나인 리지 회귀(Ridge Regression)의 방법에 대해서 간략히 살펴보겠다.
내용을 시작하기 전에 다시한 번 생각을 해보자. 과연 종속변수(Y)를 설명하는데 있어 가장 적합안 데이터 혹은 독립변수(X)는 무엇이며, 그러한 독립변수들이 Y를 어느정도로 설명하는지에 대한 비율(Coefficient 혹은 파라미터)는 어느정도여야 할 까?
아마 저 질문에 대한 답을 할 수 있다면 횡단면 분석을 이용한 데이터 분석에 있어서는 문제가 없을 거라고 본다. 우선 종속변수를 설명하는 독립변수를 선택하는것에 있어서는 개인의 역량이 중요하겠지만 이러한 변수 선택을 하는 방법의 있어서는 이후의 포스팅에서 다루어 보겠다.
본 포스팅에서 중점으로 다룰것은 바로 독립변수의 Coefficient다. 즉, 종속변수를 설명하기 위한 독립변수들의 비율을 어떻게 설정해야 될지에 대해서 다루는 것이 본 포스팅의 목적이다.
단순히 저번 포스팅에서 언급한 것처럼 종속변수와 독립변수를 나누고 Cross-Validation(교차검증)을 통해 Train Set과 Test Set을 나누어서 Error값을 가장 작게 만드는 Coefficient를 설정하는면 되지 않을까? 라는 생각이 들 수 있다.
하지만 여기서 의문이 들 것이, 단순히 그렇게 만든 모형이 최적의 모형이라고 단정지을 수 는 없다. 그 이유는 바로 Overfitting(과최적화)때문이다. 이유는 단순히 종속변수를 설명하기 위해 세상에 있는 모든 독립변수들을 사용한다면 종속변수를 설명할 수 있을 것이며 그로 인해 Train Set에 있는 Error는 줄어들 것이다(Low basis). 하지만 신기하게도 그렇게 되면 독립변수들의 Parameter의 Variance가 증가하기 때문에 Test Set을 이용해 종속변수를 예측함에 있어 불확실성이 크게 증가하는 문제점이 야기될 수 있다.
(독립변수들의 Coefficient(계수)는 어떠한 Train Set을 사용하느냐의 따라 값이 변하기 때문에 고정된 값이 아닌 변수이며, 이러한 변수들은 평균과 분산을 가지고 있는 분포를 가질 수 있다)
독립변수들의 Variance가 증가하면 무슨 문제점을 일으킬까? Variance(분산)이 크다는 것의 의미는 평균의 값보다 크게 벌어진다는 것이며 Train Set이 변할때 마다 독립변수들의 계수는 크게 변한다는 것을 의미한다.
내가 어떤 모델을 만들었고 이 모델이 안정적이라면?(모델에 있어 안정적이라는 단어가 조금은 그럴 수 있지만) 독립 변수들의 계수의 변화가 적어야 Test Set에서 예측한 값들도 어느정도 신뢰할 수 있지 않을까? 상황의 따라 계수가 무작위로 크게 변해 예측값의 안정도가 떨어진다면 모델의 대한 신뢰도는 크게 감소할 것이라고 생각한다.
따라서 선형회귀 분석을 이용해 종속변수를 설명한 독립변수들의 계수는 독립변수가 증가할 수록 계수의 분산이 증가하기 때문에 모형의 신뢰도가 많이 떨어질 수 있다는 것이다. 이것을 지난번 포스팅에서 했던 코드를 가지고 살펴볼 것이며 코드와 결과값을 보여주면서 리지 회귀분석(Ridge Regression)의 대해서도 설명하겠다.
from sklearn import datasets
boston = datasets.load_boston()
from sklearn.linear_model import LinearRegression
lr = LinearRegression() # Linear Regression 모델으리 lr 이라는 변수의 설정
lr.fit(boston.data, boston.target) # 선형회귀 분석에 분석할 데어터 설정
from sklearn.model_selection import cross_val_predict
predictions_cv = cross_val_predict(lr, boston.data, boston.target, cv=10) #Croee Validation(교차검증)을 이용해 독립변수들의 파라미터 추출

tuple_out[1]
def MSE(target, predictions):
squared_deviation = np.power(target - predictions,2)
return np.mean(squared_deviation)
MSE(boston.target, predictions_cv)
def MAD(target, predictions):
absolute_deviation = np.abs(target - predictions)
return np.mean(absolute_deviation)
MAD(boston.target, predictions_cv)
from sklearn.metrics import mean_absolute_error, mean_squared_error
print('MAE: ', mean_absolute_error(boston.target, predictions_cv))
print('MSE: ', mean_squared_error(boston.target, predictions_cv))
참고로 sklearn 모듈에서 MSE,MAD를 사용해도 되고 저렇게 함수를 만들어서 사용해도 된다.

여기까지 지난번에 포스팅 했던 방법과 결과물이다. 이번엔 무작위로 Train Set을 만들어서 그이 해당되는 선형회귀 분석의 계수들을 추출한 후 히스토그램을 그려 분포도를 살펴본다
#%% Bootstraps
n_bootstraps = 1000 # 1000번의 샘플 추출
len_boston = len(boston.target)
subsample_size = np.int(len_boston*0.5)
#무작위의 인덱스를 선택
subsample = lambda : np.random.choice(np.arange(0, len_boston), size = subsample_size)
coefs = np.ones(n_bootstraps)
for i in range(n_bootstraps):
subsample_idx = subsample()
subsample_X = boston.data[subsample_idx]
subsample_Y = boston.target[subsample_idx]
lr.fit(subsample_X, subsample_Y)
coefs[i] = lr.coef_[0]
import matplotlib.pyplot as plt
f = plt.figure(figsize = (7,5))
ax = f.add_subplot(111)
ax.hist(coefs, bins=50)
ax.set_title("Histogram if the li.coef_[0].")
plt.show()
#%%
np.percentile(coefs, [2.5, 97.5])

# 션형회귀 분석의 계수들의 분포도
from sklearn.datasets import make_regression
reg_data, reg_target = make_regression(n_samples=2000, n_features=3, effective_rank=2, noise=10)
#effective_rank = 정수 또는 None(독립 변수(feature) 중 서로 독립인 변수의 수, 만약 None이면 모두 독립)
#noise = 실수 (출력 즉, 종속 변수에 더해지는 잡음의 표준편차)
n_bootstraps = 1000
len_data = len(reg_data)
subsample_size = np.int(len_data*0.5)
subsample = lambda : np.random.choice(np.arange(0, len_data), size = subsample_size)
coefs = np.ones((n_bootstraps,3))
for i in range(n_bootstraps):
subsample_idx = subsample()
subsample_X = reg_data[subsample_idx]
subsample_Y = reg_target[subsample_idx]
lr.fit(subsample_X, subsample_Y)
coefs[i][0] = lr.coef_[0]
coefs[i][1] = lr.coef_[1]
coefs[i][2] = lr.coef_[2]
#%%
import matplotlib.pyplot as plt
plt.figure(figsize=(10,5))
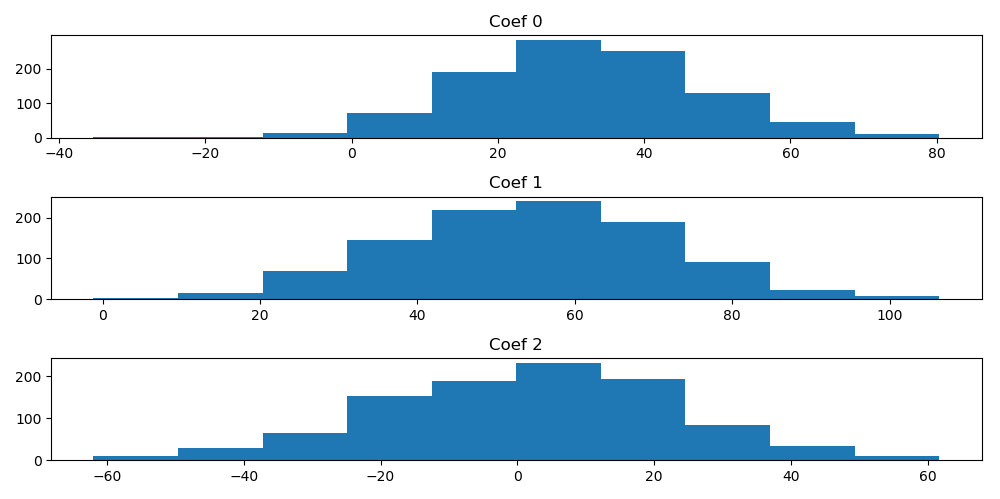
ax1 = plt.subplot(311, title = 'Coef 0')
ax1.hist(coefs[:,0])
ax2 = plt.subplot(312, title = 'Coef 1')
ax2.hist(coefs[:,1])
ax3 = plt.subplot(313, title = 'Coef 2')
ax3.hist(coefs[:,2])
plt.tight_layout()
plt.show()
#%% Ridge Regression
from sklearn.linear_model import Ridge
r = Ridge()
n_bootstraps = 1000
len_data = len(reg_data)
subsample_size = np.int(len_data*0.5)
subsample = lambda : np.random.choice(np.arange(0, len_data), size = subsample_size)
coefs_r = np.ones((n_bootstraps,3))
for i in range(n_bootstraps):
subsample_idx = subsample()
subsample_X = reg_data[subsample_idx]
subsample_Y = reg_target[subsample_idx]
r.fit(subsample_X, subsample_Y)
coefs_r[i][0] = r.coef_[0]
coefs_r[i][1] = r.coef_[1]
coefs_r[i][2] = r.coef_[2]
#%%
import matplotlib.pyplot as plt
plt.figure(figsize=(10,5))
ax1 = plt.subplot(311, title = 'Coef 0')
ax1.hist(coefs_r[:,0])
ax2 = plt.subplot(312, title = 'Coef 1')
ax2.hist(coefs_r[:,1])
ax3 = plt.subplot(313, title = 'Coef 2')
ax3.hist(coefs_r[:,2])
plt.tight_layout()
plt.show()

np.var(coefs, axis=0)
np.var(coefs_r, axis=0)

살펴보면 알 수 있지만 리지 회귀분석의 계수들의 분산이 선형 회귀분석의 계수들의 분산보다 작으며 값도 작다는 것을 알 수 있다.
다음번 포스팅에서 리지 회귀분석의 식을 통해 작동하는 원리와 파라미터를 최적화 하는 방법의 대해서 설명하겠다.
'Python > Sklearn for ML' 카테고리의 다른 글
| 5 - LASSO Regression & Parameters(라소 회귀분석에 대하여 및 파라미터 선택) using Python (0) | 2020.03.29 |
|---|---|
| 4 - Penalty(About Overfitting) (0) | 2020.03.07 |
| 3 - About Ridge Regression(리지 회귀분석에 대하여) & Optimizing the Parameter(계수 최적화) with Python (0) | 2020.03.01 |
| 1 - Linear Regression with Python(선형 직선에 데이터 적합시키는 방법) (0) | 2019.12.16 |



